사다리꼴 공식

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 성질
- 3.1. 오차 분석
4. 구현
- 4.1. 균일하지 않은 격자
- 4.2. 균일한 격자
5. 다른 수치 적분 방법과의 관계
6. 예제
참조

1. 개요

사다리꼴 공식은 주어진 구간에서 적분 가능한 함수의 정적분을 근사하는 수치 적분 방법이다. 이 방법은 적분 구간을 여러 개의 작은 구간으로 나누고, 각 구간에서 함수를 사다리꼴로 근사하여 면적을 계산하는 방식으로 작동한다. 사다리꼴 공식은 균일하지 않은 격자, 균일한 격자 모두에 적용될 수 있으며, 뉴턴-코츠 공식의 일종으로 중점 규칙과 유사한 특징을 가진다. 오차는 함수의 매끄러움 정도에 따라 다르며, 일반적으로 구간의 수(n)가 증가함에 따라 오차가 줄어든다. 주기 함수나 피크 함수에 대해 빠르게 수렴하는 경향이 있으며, 오차를 줄이기 위한 다양한 보정 방법이 존재한다.

더 읽어볼만한 페이지

수치적분 - 뉴턴-코츠 공식
뉴턴-코츠 공식은 함수의 값을 샘플링하여 다항식으로 보간하는 수치적분 방법으로 정적분의 근사값을 구하며, 폐쇄형과 개방형 공식으로 나뉘고, 룬게 현상으로 인한 오차는 합성 적분 공식을 통해 보완한다.
수치적분 - 가우스 구적법
가우스 구적법은 특정 조건을 만족하는 다항식의 영점을 노드로 사용하여 적분을 근사하는 수치 적분 방법으로, 피적분 함수에 특정 가중치를 적용, 미리 정해진 노드에서의 함수값을 사용하여 적분값을 근사하며, 다항식으로 잘 근사되는 함수에 대해 높은 정확도를 보인다.

사다리꼴 공식
개요
종류	수치 적분 방법
분야	수치 해석학
발명가	여러 명 (기원전부터 사용)
공식
일반 공식 (n+1개 지점 사용)	∫abf(x)dx ≈ (b-a)/(2n) [f(x0) + 2f(x1) + 2f(x2) + ... + 2f(xn-1) + f(xn)]
오차	- (b-a)³/12n² f'' (ξ)
파생 규칙
복합 사다리꼴 규칙	구간을 여러 개로 나누어 적용
관련 항목
관련 항목	적분 수치 적분 심프슨 공식 직사각형 공식 구적법

2. 정의

닫힌구간 $[t_0,t_N]$ 위의 적분 가능 함수 $f\colon [t_0,t_N]\to \mathbb R$ 및 수열 $t_0 \le t_1 \le \dotsc \le t_{N-1} \le t_N$ 이 주어졌다고 할 때, 적분 $F = \int_{t_0}^{t_N}f(x)\,\mathrm dx$ 의 '''사다리꼴 공식 근사'''는 다음과 같다.

: $\tilde F = \sum_{i=0}^{N-1} \frac{(t_{i+1} - t_i) (f(t_{i+1}) + f(t_i))}2$

특히, $N=1$ 일 때 사다리꼴 공식 근사는 다음과 같다.

: $\tilde F = \frac{(t_1 - t_0)(f(t_1) + f(t_0))} 2$

3. 성질

닫힌구간 $[t_0,t_N]$ 위의 적분 가능 함수 $f\colon [t_0,t_N]\to \mathbb R$ 와 수열 $t_0 \le t_1 \le \dotsc \le t_{N-1} \le t_N$ 이 주어졌을 때, 적분 $F = \int_{t_0}^{t_N}f(x)\,\mathrm dx$ 의 사다리꼴 공식 근사는 다음과 같다.

: $\tilde F = \sum_{i=0}^{N-1} \frac{(t_{i+1} - t_i) (f(t_{i+1}) + f(t_i))}2$

사다리꼴 공식 근사의 오차는 $\tilde F - F$ 로 표현된다. 사다리꼴 공식은 주기 함수를 그 주기보다 긴 구간으로 적분하는 경우 매우 정밀도가 높아지는 경향이 있는데, 이는 오일러-매클로린 공식과의 관계를 통해 이해할 수 있다. 비주기 함수에 대해서는 일반적으로 가우스 구적법이나 클렌쇼-커티스 수치 적분법과 같은 비등분점법이 더 정확하다. 이중 지수 함수형 수치 적분 공식도 사다리꼴 공식을 응용하며, 이중 지수형 함수가 들어간 경우에도 높은 정밀도를 보인다.

3. 1. 오차 분석

사다리꼴 공식 근사의 오차는 실제 적분 값과 근사값의 차이이며, 다음과 같이 표현된다.

:

\tilde F - F

f

가 2차 도함수가 존재하고 연속인

\mathcal C^2

함수라면, 다음을 만족하는

\xi\in[t_0,t_N]

가 존재한다.^[2]

:

\tilde F - F = \frac1{12}f''(\xi)\sum_{i=0}^{N-1} (t_{i+1} - t_i)^3

특히,

t_i

들이 산술 수열을 이루는 경우, 다음이 성립한다.

:

\frac1{12}\sum_{i=0}^{N-1}(t_{i+1}-t_i)^3 = \frac{(t_N-t_0)^3}{12}N^{-2}

즉,

N\to\infty

일 때, 오차는

N^{-2}

의 속도로 0에 수렴한다.

만약

f''

가 항상 양수이면 (함수가 아래로 볼록), 사다리꼴 공식 근사

\tilde F

는 실제 값

F

보다 작다. 반대로

f''

가 항상 음수이면 (함수가 위로 볼록),

\tilde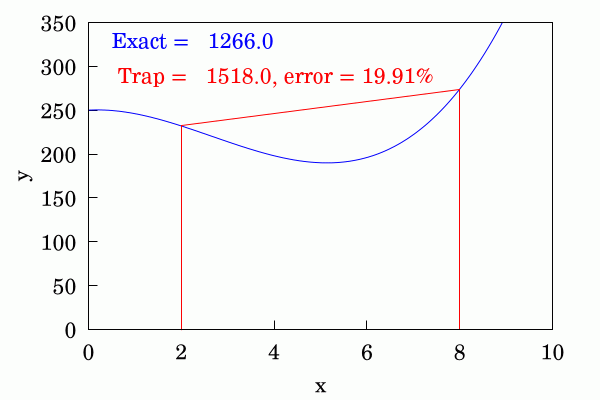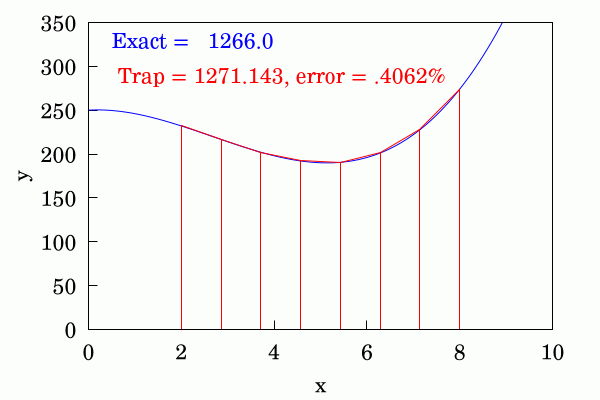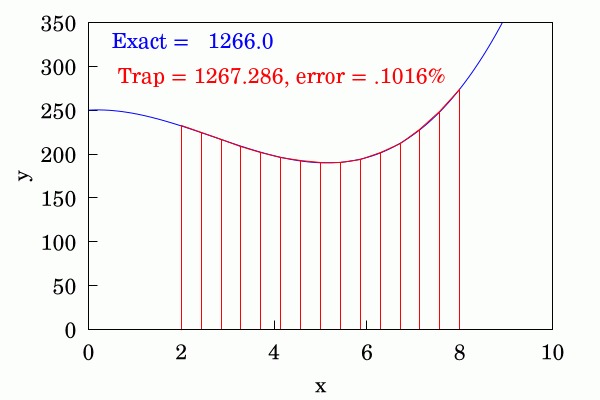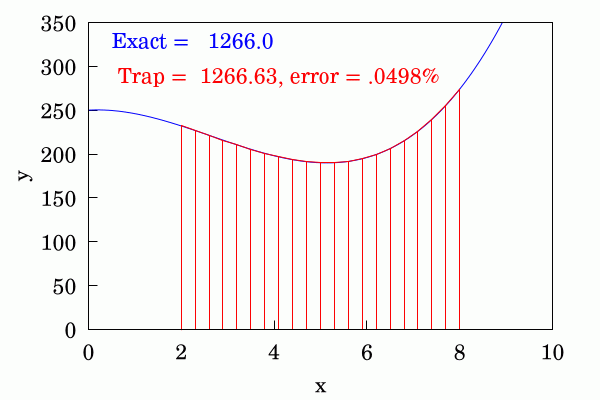 F

는

F

보다 크다.

복합 사다리꼴 공식의 오차는 다음과 같이 표현할 수 있다.

:

\text{E} = \int_a^b f(x)\,dx - \frac{b-a}{N} \left[ {f(a) + f(b) \over 2} + \sum_{k=1}^{N-1} f \left( a+k \frac{b-a}{N} \right) \right]

''a''와 ''b'' 사이에 숫자 ''ξ''가 존재하여,^[2]

:

\text{E} = -\frac{(b-a)^3}{12N^2} f''(\xi)

로 나타낼 수 있다.

N \to \infty

에 대한 점근 오차 추정치는 다음과 같다.

:

\text{E} = -\frac{(b-a)^2}{12N^2} \big[ f'(b)-f'(a) \big] + O(N^{-3}).

이 오차 추정치의 추가 항은 오일러-매클로린 덧셈 공식에 의해 주어진다.^[4]^[5]

오차 분석에 사용될 수 있는 기술은 다음과 같다.^[3]

푸리에 급수
잔차 미적분
오일러-매클로린 덧셈 공식^[4]^[5]
다항식 보간법^[6]

사다리꼴 공식은 주기 함수에 대해 빠르게 수렴한다. 이는 오일러-매클로린 공식의 결과로 설명된다.^[7] 주기성으로 인해 끝점에서의 도함수가 상쇄되어 오차가

O(h^p)

가 된다.

가우스 함수와 같이 적분 한계에서의 도함수를 무시할 수 있는 피크형 함수에도 유사한 효과가 있다.^[8] 사다리꼴 공식을 사용하여 가우스 함수의 전체 적분을 1% 정확도로 평가하는 데 단 4개의 점만 사용하면 된다.^[9]

''C''²가 아닌 함수의 경우, 위에 주어진 오차 한계는 적용되지 않지만, 이러한 함수에 대한 오차 한계를 도출할 수 있다. 이 경우, 일반적으로

O(N^{-2})

동작보다 함수 평가 횟수

N

에 따른 수렴 속도가 느리다.^[12]

사다리꼴 공식의 장점은 근사 오차를 쉽게 알 수 있다는 것이다. 볼록 함수의 적분은 실제 값보다 작은 값을, 오목 함수의 적분은 실제 값보다 큰 값을 가진다. 적분 구간에 변곡점이 포함되면 오차가 상쇄되어 전체적인 오차가 작아진다.

사다리꼴 공식의 오차 보정에는 피적분 함수의 단점에서의 고계 도함수 값을 사용한 오일러-매클로린 공식이나, 단점에서의 고계 도함수 값을 고차의 차분상으로 바꿔서 얻어지는 그레고리 공식이 알려져 있다.

4. 구현

사다리꼴 공식은 격자 간격이 균일한 경우와 균일하지 않은 경우 모두 구현할 수 있다.

4. 1. 균일하지 않은 격자

격자 간격이 균일하지 않은 경우 다음 공식을 사용할 수 있다.

:

\int_{a}^{b} f(x)\, dx \approx \sum_{k=1}^N \frac{f(x_{k-1}) + f(x_k)}{2} \Delta x_k ,

여기서

\Delta x_k = x_{k} - x_{k-1} .

4. 2. 균일한 격자

영역이

N

개의 동일 간격 패널로 이산화된 경우, 다음과 같이 정의할 수 있다.

:

\Delta x_k = \Delta x = \frac{b-a}{N}

이때 적분 근사는 다음과 같이 나타낼 수 있다.^[1]

:

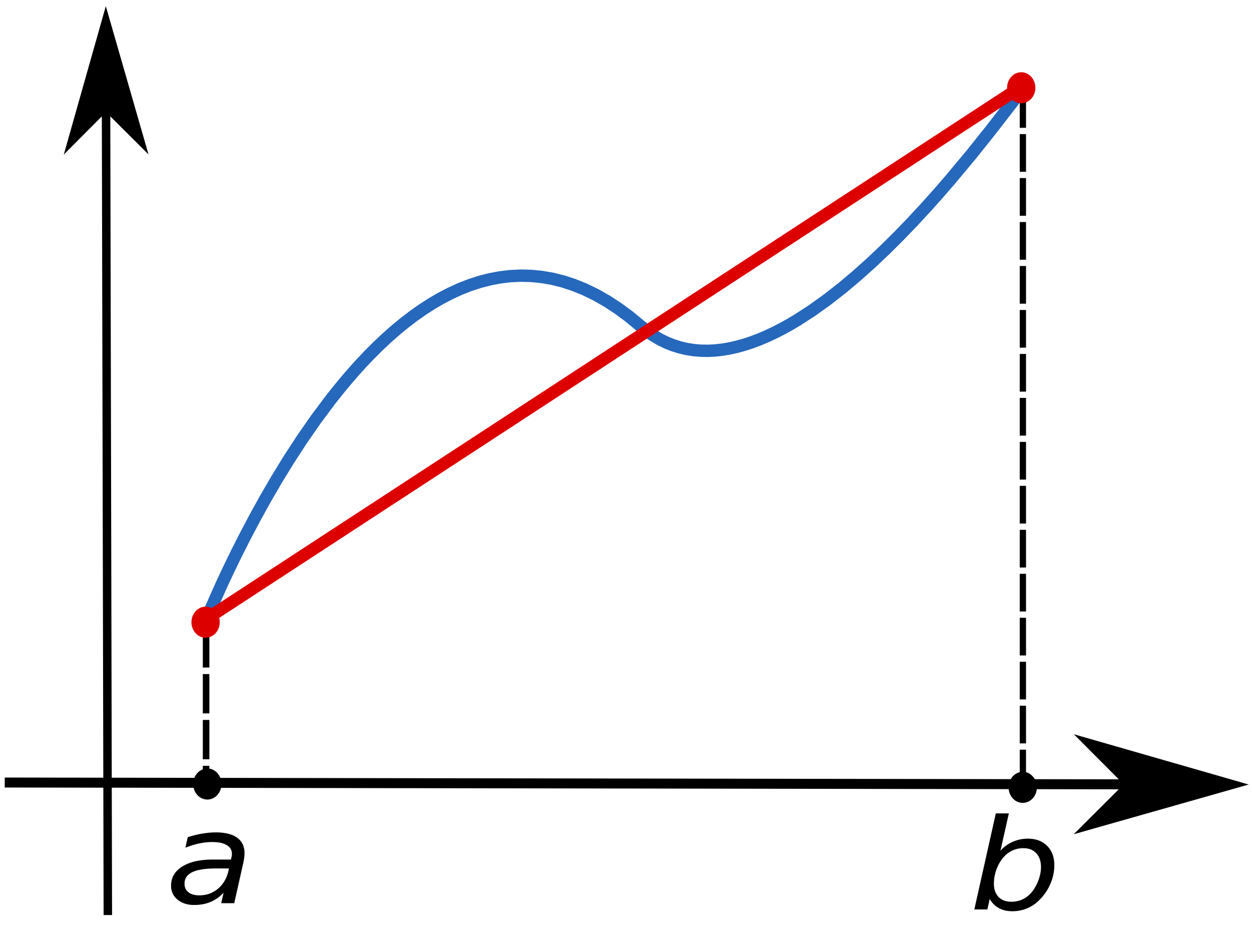
\begin{align}\int_{a}^{b} f(x)\, dx&\approx \frac{\Delta x}{2} \sum_{k=1}^{N} \left( f(x_{k-1}) + f(x_{k}) \right) \\[1ex]&= \frac{\Delta x}{2} \Biggl( f(x_0) + 2f(x_1) + 2f(x_2) + 2f(x_3) + \dotsb + 2f(x_{N-1}) + f(x_N) \Biggr) \\[1ex]&= \Delta x \left( \frac{f(x_N) + f(x_0) }{2} +  \sum_{k=1}^{N-1} f(x_k) \right)  .\end{align}

함수 ''f''(''x'') (파란색 선)을 선형 함수 (빨간색 선)로 근사

구간 폭이 일정하도록 ''k''번째 구획을 다음과 같이 설정하면,

:

a_k - a_{k-1} = \frac{b-a}{n} \quad (k=1,\dots,n)

:

a_k = a+k\frac{b-a}{n} \quad (k=0,\dots,n)

다음 공식을 얻을 수 있다.^[1]

:

\begin{align}\int_{a}^{b} f(x)\, \mathrm{d}x &\approx \sum_{k=1}^{n}(b-a)\frac{f(a_{k-1}) + f(a_k)}{2n} \\&= \frac{b-a}{2n} \sum_{k=1}^{n}(f(a_{k-1}) + f(a_k))\\&= \frac{b-a}{2n} \left(f(a_0) + 2f(a_1) + 2f(a_2)+\cdots+2f(a_{n-1}) + f(a_n) \right)\\&= \frac{b-a}{n} \left\{\frac{f(a) + f(b)}{2} + \sum_{k=1}^{n-1} f \left( a+k \frac{b-a}{n} \right) \right\}\end{align}

5. 다른 수치 적분 방법과의 관계

사다리꼴 공식은 수치 적분을 위한 공식 집합인 뉴턴-코츠 공식 중 하나이다.^[12] 심슨 공식은 같은 계열의 또 다른 구성원이며, 일반적으로 두 번 연속 미분 가능한 함수에 대해 사다리꼴 공식보다 더 빠른 수렴을 보인다. 그러나 다양한 종류의 거친 함수(더 약한 매끄러움 조건을 가진 함수)의 경우, 사다리꼴 공식은 일반적으로 심슨 공식보다 더 빠른 수렴을 보인다.^[12]

사다리꼴 공식은 주기 함수가 해당 주기에 걸쳐 적분될 때 매우 정확해지는 경향이 있다.^[13]^[14] 유사한 효과는 피크 함수에도 적용된다.^[9]^[14]

비주기 함수의 경우, 가우스 구적법 및 클렌쇼-커티스 구적법과 같이 간격이 같지 않은 점을 사용하는 방법이 일반적으로 훨씬 더 정확하다. 클렌쇼-커티스 구적법은 임의의 적분을 주기 적분으로 표현하기 위한 변수 변환으로 볼 수 있으며, 이 시점에서 사다리꼴 공식을 정확하게 적용할 수 있다.

사다리꼴 공식의 오차 보정에는 피적분 함수의 단점에서의 고계 도함수 값을 사용한 오일러-매클로린 공식이나, 단점에서의 고계 도함수 값을 고차의 차분상으로 바꿔서 얻어지는 그레고리 공식이 있다.

6. 예제

다음 적분이 주어졌다.

: $\int_{0.1}^{1.3}{5xe^{- 2x}{dx}}$

이 적분의 값을 추정하기 위해 복합 사다리꼴 공식을 사용한다. 세 개의 구간을 사용한다.

a) 참 오차 $E_{t}$ 를 구한다.

b) 절대 상대 참 오차 $\left| \varepsilon_{t} \right|$ 를 구한다.

; 풀이

a) 복합 사다리꼴 공식을 사용하여 3개의 구간을 적용한 해는 다음과 같다.

: $\int_{a}^{b}{f(x){dx}} \approx \frac{b - a}{2n}\left\lbrack f(a) + 2\sum_{i = 1}^{n - 1}{f(a + {ih})} + f(b) \right\rbrack$

여기서,

: $\begin{align}n &= 3 \\a &= 0.1 \\b &= 1.3 \\h &= \frac{b - a}{n} = \frac{1.3 - 0.1}{3} = 0.4\end{align}$

복합 사다리꼴 공식을 사용하면,

: $\begin{align}I &\approx \frac{1.3 - 0.1}{6}\left\lbrack f(0.1) + 2\sum_{i = 1}^{3 - 1}{f(0.1 + 0.4i)} + f(1.3) \right\rbrack\\&\approx \frac{1.3 - 0.1}{6}\left\lbrack f(0.1) + 2\sum_{i = 1}^{2}{f(0.1 + 0.4i)} + f(1.3) \right\rbrack\\&= 0.2\lbrack f(0.1) + 2f(0.5) + 2f(0.9) + f(1.3)\rbrack\\&= 0.2[5 \times 0.1 \times e^{- 2(0.1)}+2(5 \times 0.5 \times e^{- 2(0.5)})+2(5 \times 0.9 \times e^{- 2(0.9)}) + 5 \times 1.3 \times e^{- 2(1.3)}\rbrack\\&= 0.84385\end{align}$

위의 적분의 정확한 값은 부분 적분을 통해 구할 수 있으며 다음과 같다.

: $\int_{0.1}^{1.3} 5xe^{- 2x}{dx} = 0.89387$

따라서 참 오차는

: $\begin{align}E_{t} &= \text{참 값} - \text{근사 값}\\&= 0.89387 - 0.84385\\&= 0.05002\end{align}$

b) 절대 상대 참 오차는

: $\displaystyle \begin{align}\left| \varepsilon_{t} \right| &= \left| \frac{\text{참 오차}}{\text{참 값}} \right| \times 100\%\\&= \left| \frac{0.05002}{0.89387} \right| \times 100\%\\&= 5.5959\%\end{align}$

참조

_[1] 논문 Ancient Babylonian astronomers calculated Jupiter's position from the area under a time-velocity graph https://www.science.[...] 2016-01-29
_[2] 문서
_[3] 문서
_[4] 문서
_[5] 문서
_[6] 문서
_[7] 서적 Numerical Analysis, volume 181 of Graduate Texts in Mathematics Springer-Verlag
_[8] 논문 The evaluation of integrals of the form 1949
_[9] 논문 Comparison of integration rules in the case of very narrow chromatographic peaks 2018
_[10] 웹사이트 Euler-Maclaurin Summation Formula for Multiple Sums https://math.stackex[...]
_[11] 웹사이트 Numerical Integration over Brillouin Zones https://bandgap.io/b[...] 2017-12-19
_[12] 문서
_[13] 문서
_[14] 문서
_[15] 서적

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com